🤔 Ever wondered how elevators, traffic lights and vending machines work? Look no further! Finite State Machines (FSMs) are the secret ingredient to their smooth functioning. In this article, we dive into the world of FSMs and discover why they're so powerful in modelling and designing systems. 💡 From understanding the behaviour of NPCs in games to automating business processes, FSMs are the key to making it all happen. 🚀

Finite State Machine

A Finite State Machine (FSM) is a mathematical model of computation that is used to design and implement software systems. It is a powerful tool for modelling systems that have distinct states and transition between those states based on certain inputs. The key idea behind an FSM is that the system's behaviour is determined by its current state and the inputs it receives. The system's next state is determined by the current state and the input, this transition is defined by a set of rules. Finite state machines have a finite number of states, which makes them well-suited for solving problems that can be broken down into a limited number of distinct states. They are widely used in various applications such as digital logic design, compilers, network protocols, and user interfaces.

Traffic lights example

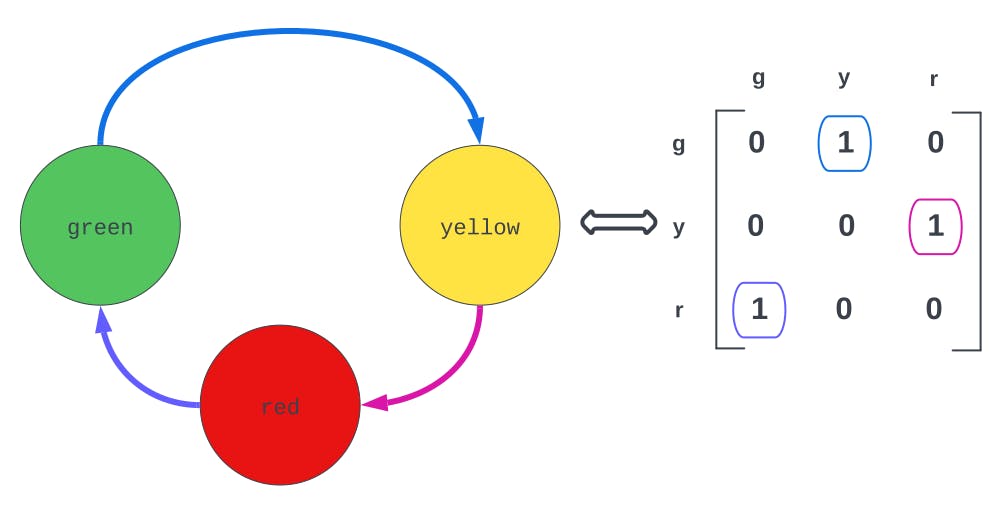
This might look not so clear at the first glance so let's start with an example from the real world - traffic lights🚦. The transitions between states are determined by the inputs received by the traffic light. For example, when the traffic light is in the 🟢 (green) state, it will receive an input to change to the 🟡 (yellow) state after a certain amount of time. Then, it will receive an input to change to the 🔴 (red) state.

Please note that traffic light transitions might be different across the globe.

The finite state machine of a traffic light can be represented as follows:

🟢 (green) ---> 🟡 (yellow) ---> 🔴 (red) ---> 🟢 (green)

or as a directed graph which could also be a matrix:

In a matrix representation of a graph, each row represents a node, and each element represents a directed and weighted edge. Edges with a weight of zero are not included. The element located in the i-th row and j-th column corresponds to an edge going from the node i to node j. This type of graph is known as a directed graph or digraph. Please note that as weights of the edges aren't giving any additional information in FSM so for ease of representation they're weighted as 1.

But why?

Because it provides a clear and formal way to model the behaviour of the traffic light system. With an FSM, the different states of the traffic light, as well as the inputs that trigger transitions between those states, can be easily understood and implemented. This makes it simple to design, implement, and maintain the traffic light system, which is especially important when it is integrated with other systems.

Alternatively, traffic lights can be modelled using other techniques such as rule-based systems, decision trees, or neural networks. However, these methods can be more complex and harder to understand and maintain than an FSM, especially in the case of large and complex systems. Additionally, they may not provide the same level of simulation and analysis capabilities as an FSM.

Use cases

Finite state machines (FSMs) are a powerful tool for modelling and designing systems that have a finite number of states and well-defined transitions between those states. Here are a few examples of when using an FSM could be a good idea:

1. Control systems 🚀: FSMs are commonly used in control systems to model the behaviour of devices such as elevators, traffic lights, and vending machines. These systems have a finite number of states and well-defined transitions between those states, making them a good fit for an FSM.

2. Communication protocols 📡: FSMs are also used in the design of communication protocols such as TCP/IP and USB. These protocols have a finite number of states and well-defined transitions between those states, making them a good fit for an FSM.

3. Game development 🎮: FSMs are often used in game development to model the behaviour of non-player characters (NPCs) and other entities. For example, an NPC may have different states such as idle, walking, attacking, and dying.

4. Robotics 🤖: In robotics, FSMs are used to control the movement, sensing, and decision-making of robots.

5. Natural Language Processing (NLP)📝: In NLP, FSM is used to model the different states of words, phrases, and sentences.

6. Business Process Automation 💼: FSMs are used in business process automation to model the flow of a process, from initiation to completion.

Generally, FSMs are particularly useful when the system has a finite number of states and well-defined transitions between those states.

Python libraries for FSM

Here are the two most popular Python libraries that can be used to implement FSM:

1. transitions:[~4.7k ☆] github.com/pytransitions/transitions This library provides a simple and easy-to-use API for defining states, transitions, and callbacks. It supports the definition of states and transitions using classes and provides a simple syntax for defining triggers and callbacks. It also supports the definition of nested states and parallel states. Additionally, it provides a variety of ways to visualize and debug the state machine.

2. python-statemachine:[~300 ☆] https://github.com/fgmacedo/python-statemachine This is a powerful and intuitive state machine framework that allows for the easy creation of complex, dynamic systems with clean, readable code. It promotes understanding and reasoning about states, events, and transitions, and provides robust error handling to keep systems in a valid state.

Summary

In summary, Finite State Machines (FSMs) are mathematical models of computation that can be used to design and implement software systems. They are powerful tools for modelling systems that have distinct states and transitions between those states based on certain inputs. An example of this is traffic lights, which have a finite number of states and well-defined transitions between those states, making them a good fit for an FSM. The key benefit of using an FSM is that it provides a clear and formal way to model the behaviour of a system, making it simple to design, implement, and maintain. FSMs are widely used in various applications such as digital logic design, compilers, network protocols, and user interfaces. Additionally, they can be used in control systems, communication protocols, game development, robotics, natural language processing, and business process automation.

---

tl;dr

1. Finite State Machines (FSMs) 🤔 are mathematical models of computation that can be used to design and implement software systems.

2. FSMs are powerful tools for modelling systems that have distinct states and transitions between those states based on certain inputs.

3. FSMs are widely used in control systems 🚀, communication protocols 📡, game development 🎮, robotics 🤖, natural language processing 📝, and business process automation 💼